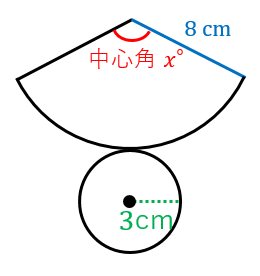
半径rが1、中心角θが60 の扇形の面積 面積 S: 円弧の長さ L: 弦の長さ a:1 面積の計算 ・正三角形の面積 ・三角形の面積(底辺と高さ) ・三角形の面積(2辺と間の角度) ・三角形の面積(1辺と両端の角度) 以下の計算式を参考にして 底面の半径が3cmなので、円周=直径× π =6 πcm となります。 底面の円周とおうぎ形の孤の長さは等しいので、孤の長さも6 π cmです。 そこから、半径12cm&孤の長さ6 π cmのおうぎ形の中心角を逆算して求める──これが一般的な解き方です。 半径をr、中心角をθ、弧の長さをL、面積をSという文字にします。 円周の長さは直径×円周率(2rπ)ですよね? つまり円弧の長さは中心角との比と考える事ができるので L=2rπ×θ/360 また円の面積は半径×半径×円周率(πr^2、^2は2乗)で

円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者
おうぎ形 中心角 求め方 半径と面積
おうぎ形 中心角 求め方 半径と面積- 中心角/360=弧の長さ/円周 や 中心角/360=おうぎ形の面積/円の面積 という方程式を書くことでも解けるよ。 おうぎ形の計算は公式とこのやり方の2つを覚えていれば、 だいたい解けるようになっています。(弧の長さ)= (半径)× (円周率)× (中心角)÷180




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット
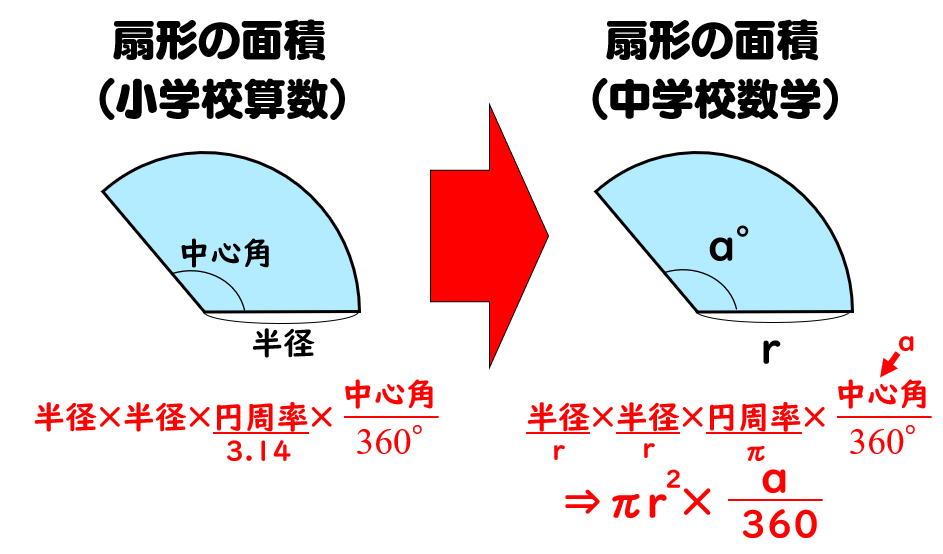
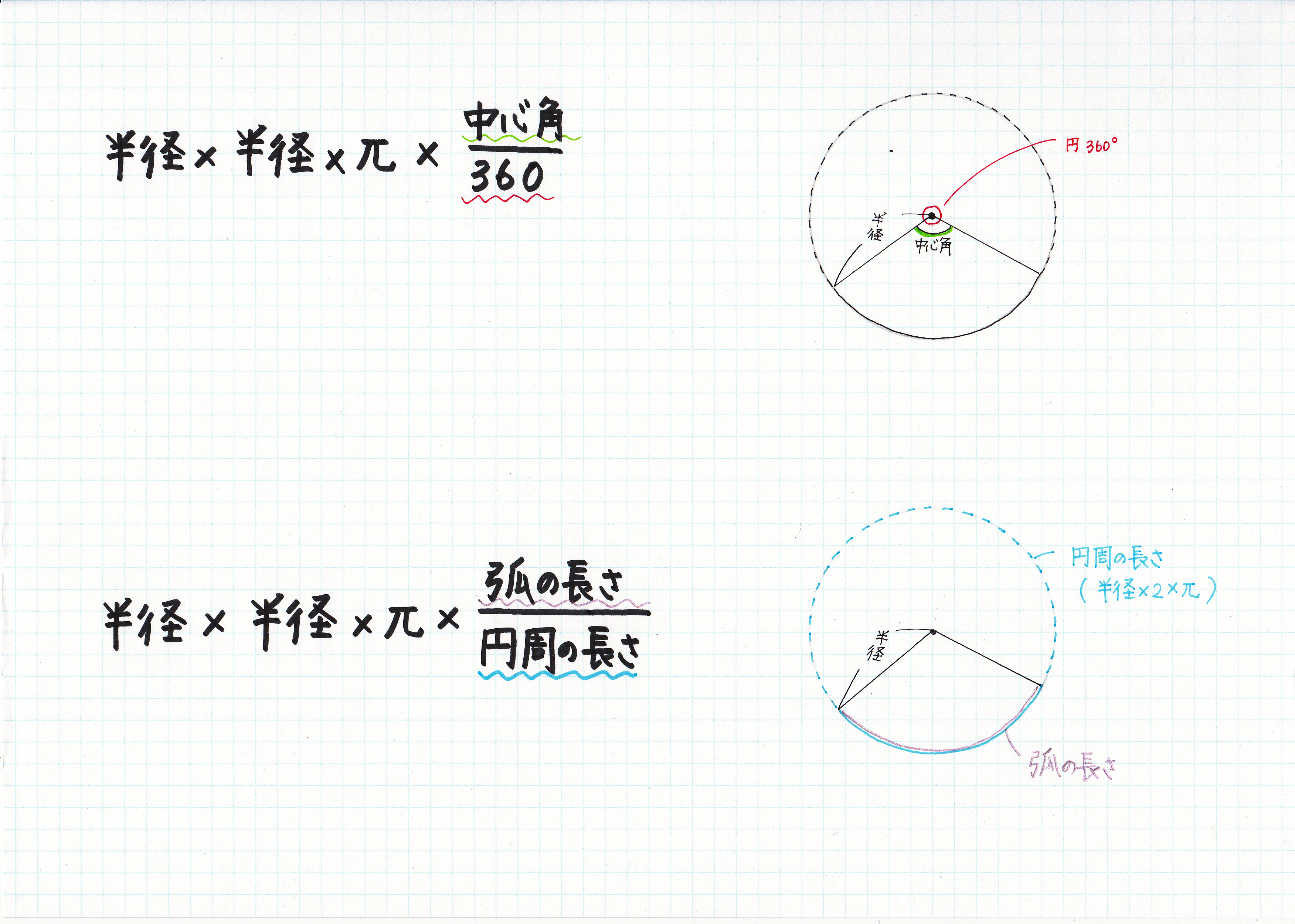
おうぎ形の弧の長さや面積は中心角に比例するので, おうぎ形の弧の長さや,面積を求めるには, 円周の長さや,円の面積に 中心角 360° をかければよい。 半径rで中心角がaのおうぎ形 弧の長さ l = 2πr × a 360 面積 S = πr2 × a 360 例半径18cm, 中心角40°の 求めたい半径の大きさを ㎝とすると 半径が ㎝で中心角が1°の扇形の面積は と、表すことができます。 そして、面積が ㎠になるはずだから という二次方程式が完成します。 あとは、これを解いていけば の値(半径)を求めることができます。 この面積を使った中心角の求め方 おうぎ形の面積と半径 がわかっていれば、中心角の大きさを求めることができます。 おうぎ形の面積の公式は以下でしたね。
↓ ↓ ↓ ↓ ↓ ↓https//studyline32com/l/u/6XQOiYkgoDeSmFNm中1で学習する平面図形の単元から「おうぎ形の中心 中心角・弧・面積の求め方 おうぎ形における中心角・弧・面積という3点セット。 これらの求め方は今言ったように、 どれか1つから \(\frac{\mbox{おうぎ形}}{\mbox{円全体}}\) という割合を出す;この、中心角の求め方を教えてください。 (1)の方です 3 半径が 6cm, 面積が 12zcm2のおうき形がある Q) 中心角の大きさを求めなさい。 (2
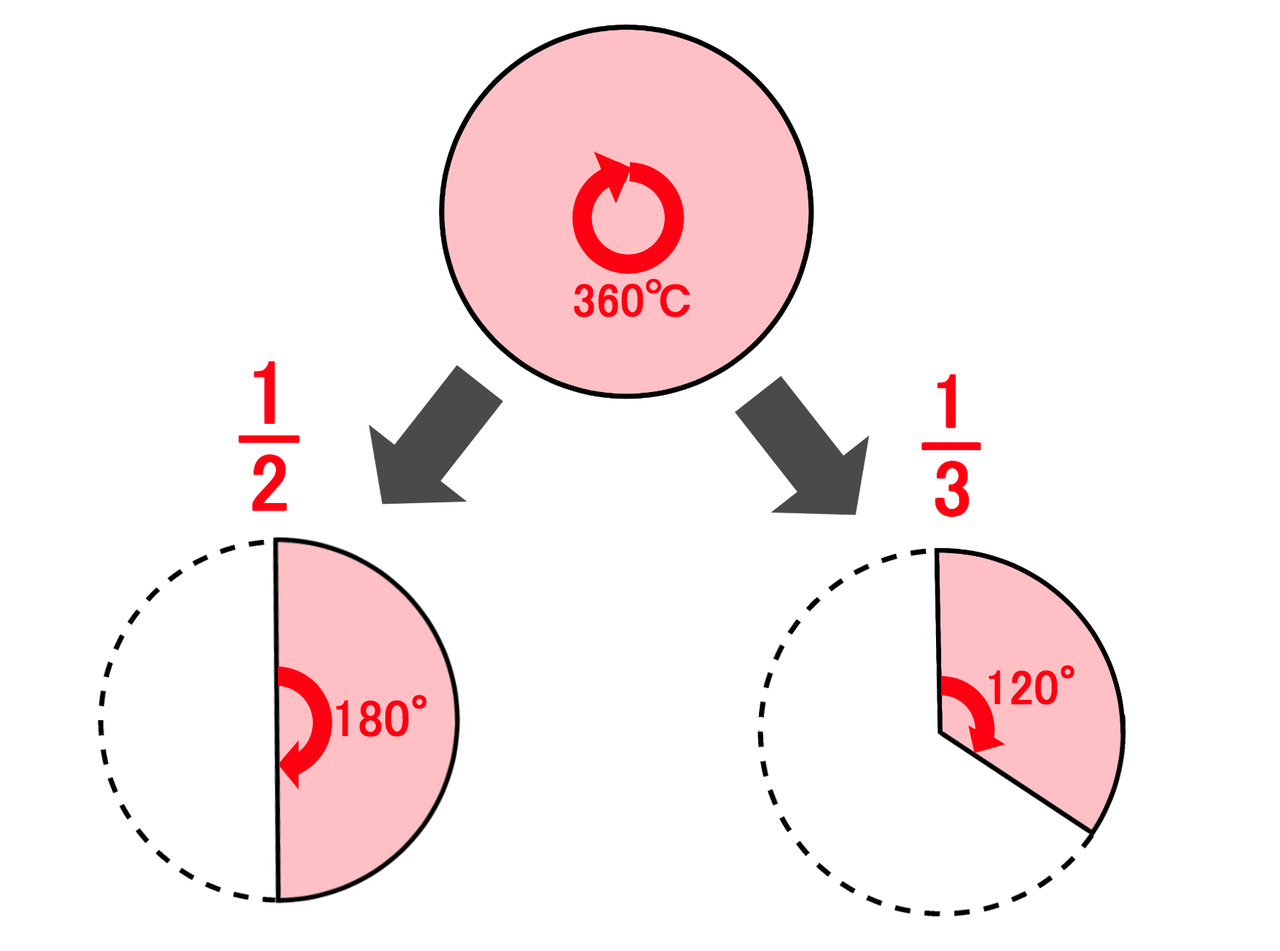
問題 面積がπ㎝²、中心角が40°であるおうぎ形の半径を求めなさい。 今度は面積が与えられているので おうぎ形の面積の公式に当てはめていきましょう。 すると、このような方程式ができあがります。 これを解いていきましょう! 両辺をπで割って おうぎ形の弧の長さ、面積、中心角の求め方と公式 おうぎ形は円を切りとったものです。 半分だけ切りとれば中心角は180°、さらに半分切りとれば中心角は90°になります。 ケーキを半分に切ったり、三分の一にしたりするときを想像するとわかりやすいでしょう。 おうぎ形の弧の長さと面積は下のプリントのように求めます。 半径をr、中心角をa°とします。 弧円の面積を求める公式は、次の通りです。 円の面積 = 半径× 半径×314 円の面積 = 半径 × 半径 × 31 ;




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者
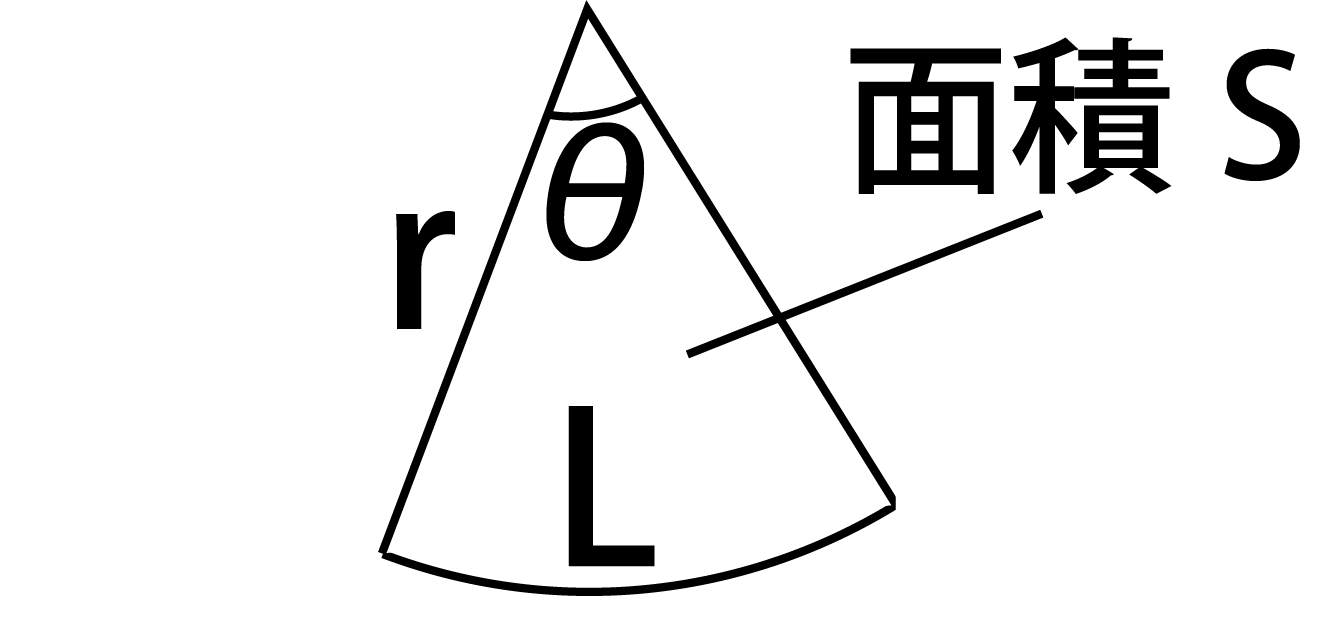



扇形の面積公式が一目でわかる 丁寧な証明付き 高校生向け受験応援メディア 受験のミカタ
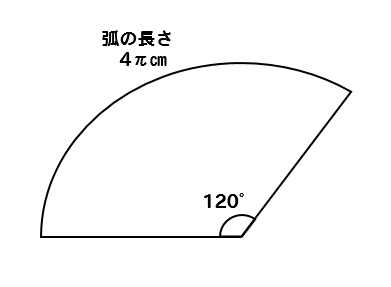
目次 平面図形の面積の求め方の公式 台形=(上底+下底)×高さ÷2 ひし形(対角線直交四角形)の面積=対角線×対角線÷2 円周=直径×円周率(314)=半径×2×円周率(314) 円の面積=半径×半径×円周率(314) おうぎ形の弧の長さ=円周×中心角/360半径5cmで中心角30°のおうぎ形の弧の長さを求めよ。 半径16cmで中心角315°のおうぎ形の弧の長さを求めよ。 半径12cmで中心角80°のおうぎ形の面積を求めよ。 半径10cmで中心角°のおうぎ形の 問題文に面積が与えられているので、円と扇形の面積を比較しながら中心角を求めます。 半径が4㎝の円の面積は、\(\pi\times 4^2=16\pi(cm^2)\) 半径が4㎝の扇形の面積は、問題文より \(4\pi(cm^2)\) です。



おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ




1 6 C111 24 Cm Descubre Como Resolverlo En Qanda
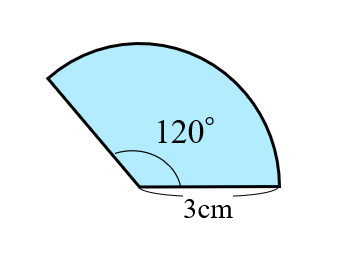
これには、2通りのやり方がある。 問3半径6cm、弧の長さ8πcmのおうぎ形の中心角と面積を求めなさい。93.おうぎ形の面積 下の図のような、半径がcm、中心角が144°のおうぎ形があります。 点エ、オ、カ、キ、ク、ケ、コは、おうぎ形の弧イウ(曲線の部分 おうぎ形の面積は3πで中心角は x です。 それに対して、同じ半径 (3㎝)を持つ円の面積と中心角を考えると9πと360°になります。 ※円の中心角は常に360°です。 半径をr、面積をS、円周率をπ、中心角をαとすると、 S = πr² × α / 360




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ
おうぎ形の面積を求める公式は \ おうぎ形の面積 = 円の面積 \times \frac {中心角} {360°} \ なので、円の半径を \ (r\) とするとおうぎ形の中心角を求める問題で,わかっている数字が変わると求め方がわからなくなります。 ※ このQ&Aでは、 「進研ゼミ中学講座半径の長さ6㎝、中心角 教科書124ページの例2を使って、おうぎ形の弧の長さと面積の求め方を確認す ・おうぎ形の中心角の大きさの求め方を理解する。面積や弧の長さを求める問題にも対応できるようになるよ じゃあ、具体的に見ていこうね 具体的に解く 中心角の求め方の問題は3パターン考えられるよ 弧の長さと半径が分かっている場合 面積と半径が分かっている場合 弧の長さと



扇形とは 面積 中心角 半径 弧の長さの公式と求め方 受験辞典



半径8cm 中心角135 のおうぎ形の弧の長さと面積を求めてくださ Yahoo 知恵袋
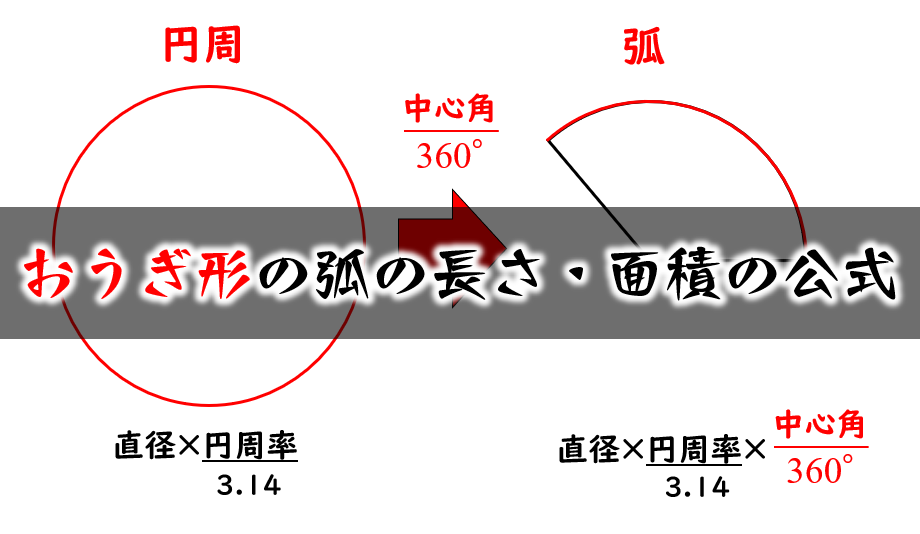
扇型の求め方や中心角の求め方も分からないので 解説もお願いします😓 この問題の答えは 『27π』になります (0 右の図は底面の半径が 3 cm で, 母線の長さが 6 cm の円すいである。 この円すいの表面積は cm' である。 では、面積も求めていきます。円周上に $2$ 点 ($\rm A,B$) をとる。このとき、$\rm A$ から $\rm B$ までの円周上の部分を 弧 といって、$\textcolor{blue}{\stackrel{\frown}{\rm AB}}$ とかきます。 この 弧 と $\textcolor{blue}{2}$ 本の半径 で囲まれた図形を おうぎ形 といいます。 ちなみに、$\rm ∠AOB$ は 中心角 といい、線分 $\rm AB$ は 弦 といいおうぎ形の弧の長さや面積を求めるには求めるおうぎ形が 円のどのくらいの割合であるかがわかればよい 〈重 要〉 ・半径rcm、弧の長さℓcm のおうぎ形の面積の求め方 おうぎ形の性質「おうぎ形の弧の長さは中心角に比例する」を利用して




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット



扇形とは 面積 中心角 半径 弧の長さの公式と求め方 受験辞典
右の図は,円 錐 すい の展開図であり,側面となるおうぎ形は,中心角が135°で面積が ㎝ 2 である。この円錐の底面となる円の半径の長さを求めなさい。 おうぎ形 中心角 求め方 面積 おうぎ形 中心角 求め方 面積この2つさえ覚えていれば、中心角を求めるだけじゃなくて 面積や弧の長さを求める問題にも対応できるようになるよ じゃあ、具体的に見ていこうね 具体的に解く 中心角の求め方の問題は3 これで中心角が分からなくても母線 x と弧の長さ z さえわかればおうぎ形の面積を求められます。 あとはこの式を整理すると、、、 よって、おうぎ形の面積は 「母線の長さ × 弧の長さ ÷ 2」 で求めることができるというわけですね。 tagPlaceholder



Q Tbn And9gcqfv9ekt Crg9bhcsz7q4t2e8znl6v2tplsqinzmz3lidwdpywk Usqp Cau




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
扇形の面積と弧の長さがわかっているときの、扇形の角度の求め方を教えてください。 〔回答〕 以下の説明において、 S=おうぎ形の面積,ℓ=弧の長さ,r=おうぎ形の半径,x=中心角の大きさ とします。 まず、おうぎ形の面積に関しては (1おうぎ形の面積を求める公式は \ おうぎ形の面積 = 円の面積 \times \frac{中心角}{360°} \ なので、円の半径を \(r\) とするとおうぎ形の中心角を求める問題で,わかっている数字が変わると求め方がわからなくなります。 円とおうぎ形 中学受験準備のための学習ドリル Study 円錐の側面 扇形 の中心角の求め方 中2数学 ちくらっぽインク 簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく 数学 円すいの展開図 扇形の中心角は5秒で出せる 受験




扇形の面積の求め方 公式と計算例




円 扇形 の面積 周や弧の長さの公式 数学fun
半径 5cm, 面積 πcm 2 のおうぎ形の弧の長さを求めよ。 半径4cm,弧の長さ6πcmのおうぎ形がある。 面積を求めよ。 中心角を求めよ。おうぎ形の中心角の求め方 まとめ おうぎ形の中心角を求める方法は大きく分けて3つのパターンがありました。扇形の面積・弧の長さ・まわりの長さの求め方公式 =直径×円周率× 中 心 角 360 ° +半径×2 ピタグラスの定理(三平方の定理)により,横の長さが Δx,縦の長さが Δy である直角三角形の斜辺の長さ ΔL は したがって x ,y 直交座標では x=t とおけば上記の公式が得られる.・円弧の長さは rθ 円周の長さ 2πr に対して、中心角の割合が θ/2π であるため もしくは、単純に、1ラジアンの円弧の長さ(=半径(r))の θ倍であるため ・扇形の面積は (r 2 θ)/2円弧三角計算 半径、中心角(DMS形式orDEG形式)、弦長、弧長、高さ、底辺1、底辺2、円弧高を求める計算です。




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット




扇形の面積の求め方 公式と計算例
半径8センチ,面積48πcm²の おうぎ形の中心角を求めなさい という問題なんですが この求め方が分からないので 教えてください! ぶいまたく より 18年2月11日 1221 PM 半径8cm、弧の長さ4πcmのおうぎ形の面積は、中心角をa°として 4πcm=2×π×6×a/360 a=4π/12π×360=1 よって中心角は1°となりますが、4π/12π×360という式を理解してもらえません。 数学・算数 おうぎ形 おうぎ形の面積っていうのは、半径X半径X中心角/360ですよね? それと周の求め方は直径×中心角/360



扇形の中心角の求め方を教えてください 中心角の求め方は2通りのパタ Yahoo 知恵袋



円錐の母線 半径 中心角の関係式とそれぞれの求め方 具体例で学ぶ数学
半径 3 3 cm、中心角 1° 1 ° のおうぎ形の弧の長さと面積を求めよ。 弧の長さ:3×2×314× 1 360 1 360 =3×2×314× 1 3 1 3 =2×314=628( cm c m ) 面積:3×3×314× 1 360 1 360 =3×3×314× 1 3 1 3 =3×314=942 (cm2 c m 2) おうぎ形の面積の求め方2 もう一つのおうぎ形の面積の求め方は円の面積を求めてから、そこから中心角を用いておうぎ形を求める方法です。 まずは簡単におうぎ形の中心角が $60^{\circ}$ の場合を考えます。




7 Times2 Descubre Como Resolverlo En Qanda




円 扇形 の面積 周や弧の長さの公式 数学fun




おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ




平面図形 おうぎ形の中心角の求め方 中学数学 定期テスト対策サイト



1
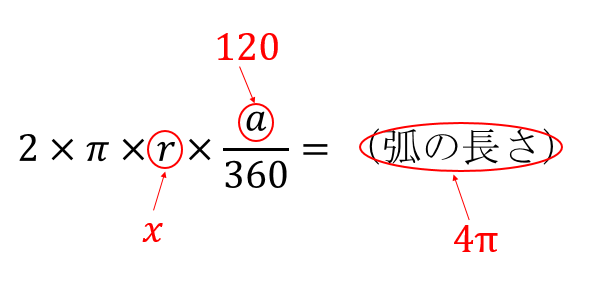



おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ




弧の長さを使った扇 おうぎ 型の面積の公式を知っていますか



円 扇形 の面積 周や弧の長さの公式 数学fun




円錐の母線 半径 中心角の関係式とそれぞれの求め方 具体例で学ぶ数学



扇形とは 面積 中心角 半径 弧の長さの公式と求め方 受験辞典




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者




おうぎ形の弧の長さ 面積 中心角の求め方と公式 Irohabook




中1 数学 空間図形9 おうぎ形の公式 17分 Youtube




これの表面積の求め方の解説をお願いしたいです W Clear



おうぎ形の弧の長さと面積の求め方 小学生に教えるための解説 数学fun



3




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者




おうぎ形 弧の長さ 面積 中心角の求め方 学習内容解説ブログ




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット




中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく




円錐の側面積 展開図の扇形の中心角 半径 母線を軸として解く 身勝手な主張




おうぎ形の中心角の求め方 Youtube




中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく




中1数学のおうぎ形の公式が覚えられません そろそろテストなのでやばいんです 今はとに Clear
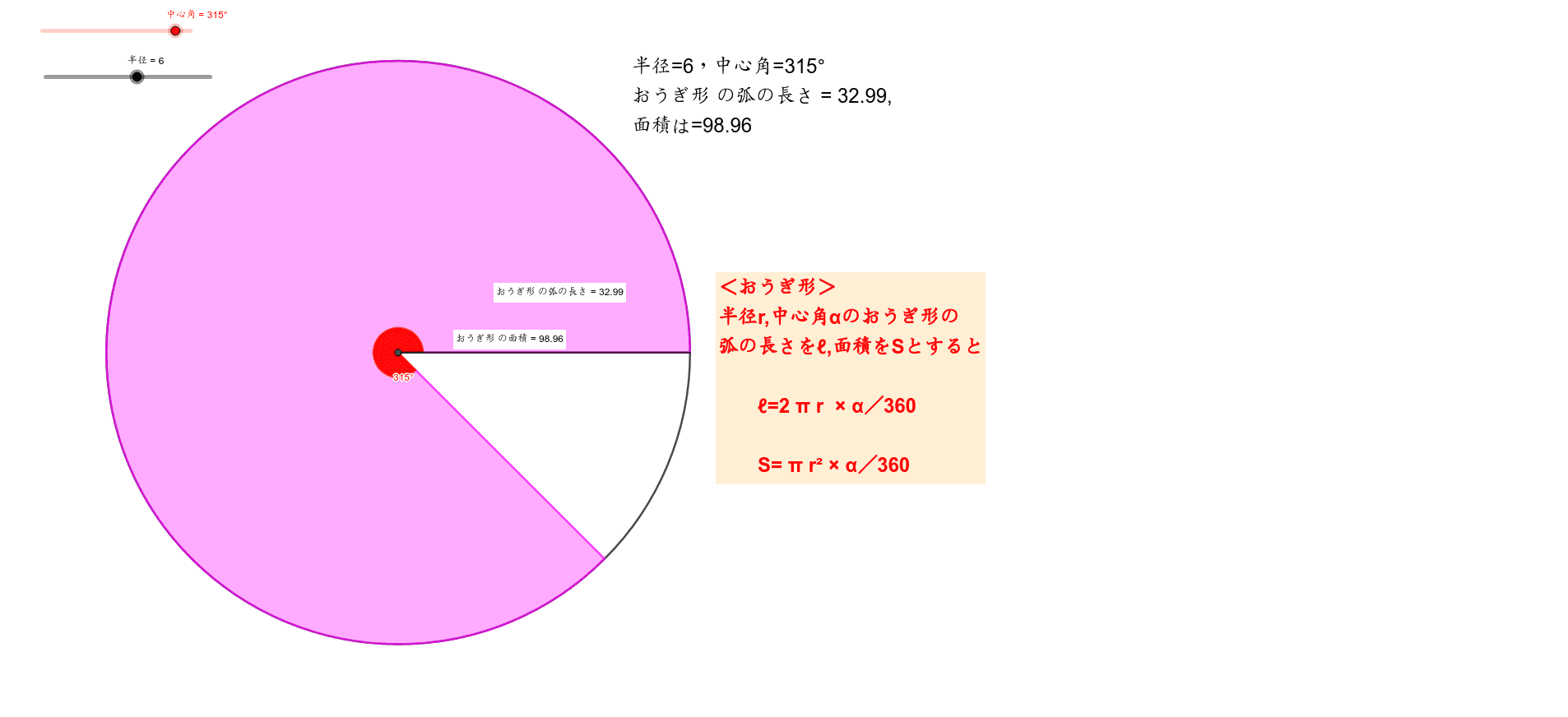



中1 おうぎ形の弧の長さや面積について考えよう Geogebra




扇形の面積の求め方 小学生でも公式を簡単に使える問題です 中学や高校の数学の計算問題




円錐の表面積 中心角を求める問題を丁寧に解説 数スタ




半径6cm 面積18pcm の扇形の中心角の求め方を教えて欲しいです Clear




おうぎ形の面積と弧の長さの公式 全国 中学数学ができるようになるブログ




扇形の弧の長さの公式 簡単な問題で求め方をマスターしよう 中学や高校の数学の計算問題



ダウンロード 扇形 中心 角 求め 方 ニスヌーピー 壁紙



おうぎ形の弧の長さと面積の求め方 小学生に教えるための解説 数学fun




おうぎ形の面積 弧度法との関連から眺める 身勝手な主張



1




半径6cm 弧の長さ2pcmのおうぎがたの面積 はどーやって求めますか Clear



おうぎ形の面積と弧の長さの求め方 バカでもわかる 中学数学



おうぎ形の面積の公式について 現役塾講師のわかりやすい中学数学の解き方




3分で分かる 扇形 おうぎ形 の面積と弧の長さの求め方 公式をわかりやすく 合格サプリ




扇型の求め方や中心角の求め方も分からないので 解説もお願いします この問題の答えは Clear




おうぎ形の問題 パターンを知ろう 苦手な数学を簡単に




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




おうぎ形の弧長 面積 中心角 半径 具体例で学ぶ数学



中学 数学です 中心角150度 弧の長さ5pcmのおうぎ形の半径 Yahoo 知恵袋




中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく




おうぎ形の弧の長さと面積の求め方 小学生に教えるための解説 数学fun
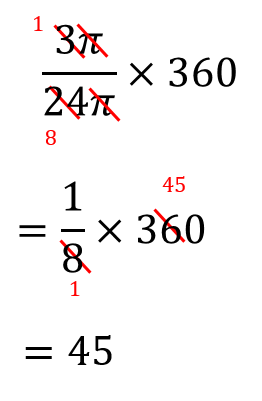



おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ



おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ




中1です お願いがあります 扇形の中心角の求め方を Clear




中1 数学 中1 75 おうぎ形の弧と面積 基本編 Youtube




扇形の面積の出し方と特殊な場合の公式 たぬぬ塾 中学校の先生たち




おうぎ形 半径の求め方 数学の記録




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ




Kelas 7 Catatan Tentang 中1 数学 範囲 Clear




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
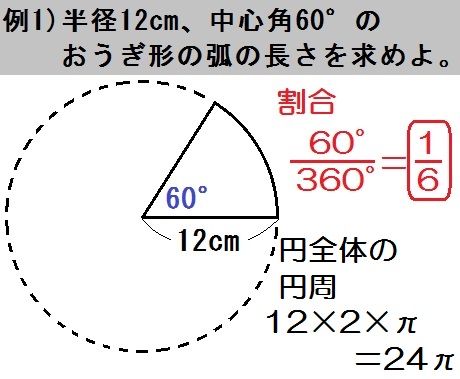



中学数学 平面図形 のコツ 円とおうぎ形




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



Squaresqrte 15 1 5 18 2 Descubre Como Resolverlo En Qanda




印刷可能 円錐 中心角 求め方 比




公式を図解 すい体の体積 円すいの表面積の求め方




扇形の弧の長さと面積 小学 中学数学での平面図形の求め方 リョースケ大学
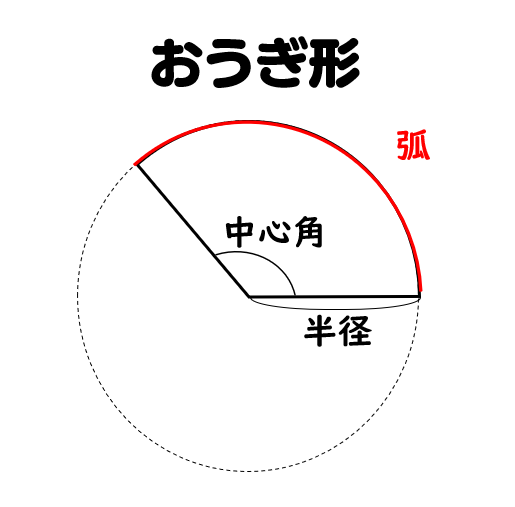



おうぎ形の弧の長さと面積の求め方 小学生に教えるための解説 数学fun




おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ




おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ



半径4cm 中心角225 のおうぎ形の弧の長さと面積の求め方と答 Yahoo 知恵袋




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



扇形とは 面積 中心角 半径 弧の長さの公式と求め方 受験辞典




裏技 おうぎ形の面積を一瞬で求める 弧の長さを利用した裏技公式 中学数学 平面図形 2 Youtube




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ




中1数学 おうぎ形の公式 練習編2 映像授業のtry It トライイット




おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ




円とおうぎ形の周りの長さ 面積の求め方 無料プリントあり




おうぎ形の弧の長さと面積の求め方 小学生に教えるための解説 数学fun




中学1年生 数学 円とおうぎ形 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



半径9cm 面積18pcm の扇形の中心角を求めなさいという問 Yahoo 知恵袋




円 扇形 の面積 周や弧の長さの公式 数学fun




この周の長さが12p 12 Cm なのですが分からないので解き方を教えてください Clear



半径15cm 弧の長さ12pcmのおうぎ形について 中心角の大 Yahoo 知恵袋




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



扇形とは 面積 中心角 半径 弧の長さの公式と求め方 受験辞典




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




扇形の弧の長さと面積 小学 中学数学での平面図形の求め方 リョースケ大学




扇形の中心角の求め方を教えてください Clear




おうぎ形の弧の長さ 面積 中心角の求め方と公式 Irohabook




円とおうぎ形 中学受験準備のための学習ドリル




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット




中学数学 おうぎ形の中心角を求める問題 Youtube



0 件のコメント:
コメントを投稿